Ir al contenido principal
BrainMatics. Rompecabezas lógicos.
Ivan Moscovich
h.f.ullmann. 2009
Páginas 100 y 101.
EL NÚMERO π Y LA CIRCUNFERENCIA DE UN CIRCULO
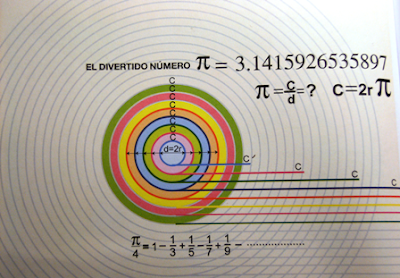
π no es un número normal. Es especial y se encuentra en los lugares más insospechados. Como la extraordinaria relación existente entre π y los números impares. ¿Qué tuvieron que ver los círculos que pueden encontrarse en la Tierra con los números impares? Su historia se remonta cuatro mil años atrás y su estudio revela la belleza inherente a las matemáticas. El símbolo que lo representa es una letra del alfabeto griego. Fue introducido por Leonhard Euler, ¡cómo no!, el gran matemático suizo. Debido a que el círculo desempeña una importante función en tantas cosas, en matemáticas, en las ciencias, y en la vida diaria, bien vale la pena conocerlo, pero, ¿qué es π «exactamente»?
π representa la relación de la circunferencia de un círculo con su diámetro. π siempre es el mismo número, independientemente del tamaño del círculo.
Esta relación es uno de los números constantes más fascinantes de la larga historia de las matemáticas.
π SEGÚN EL MÉTODO DE ARQUÍMEDES
El método de Arquímedes para la estimación del número
π se basa en inscribir y circunscribir polígonos regulares (polígonos con lados de igual longitud) en un círculo con un diámetro de una unidad (o un radio de la mitad de una unidad). Los perímetros de los polígonos inscritos y circunscritos hacen de límites mínimo y máximo, respectivamente, del valor de
π . Arquímedes tuvo que crear construcciones geométricas y utilizar este método en un polígono regular de 96 lados, y pudo determinar que
π estaba entre 3 10/71 y 3 1/7 o entre
3,14084 y 3,14285.
Si Arquímedes hubiera hecho la media entre estos límites, habría obtenido
π =3,141845 con una sorprendente precisión de un 99,99%.
Páginas 104 y 105.
EL ÁREA DEL CÍRCULO Y π
El problema de determinar el área de un círculo fue un gran reto matemático que Arquímedes (287- 212 a.C.) intentó resolver. Intentó resolverlo con el método de la «cuadratura del círculo», es decir, en-contrar un cuadrado (polígono) que tuviera la misma área que un círculo de un radio determinado. Su método, que dio lugar a La fórmula exacta, se ha demostrado.
El círculo de radio r se divide en un gran número de triángulos casi isósceles con lados r y bases a (pequeños arcos circulares próximos a líneas rectas), que se pueden disponer de manera que formen un paralelogramo, tal y como aparece en la figura. En cuantos más sectores se divida el círculo, más se parecerán los sectores a triángulos, que cada vez son más pequeños, y la figura se aproxima a la forma de un rectángulo. La altura de cada triángulo es casi la misma que el radio del círculo r. La circunferencia del círculo = 2 x r x π . Cada color de los triángulos cubre la mitad de la circunferencia del círculo, de manera que la longitud del rectángulo es la mitad, es decir, π x r. De ahí que: área del círculo = área del rectángulo (que se muestra) = altura x anchura r x (π x r) = π x (r al cuadrado), que es la famosa fórmula que conocemos hoy en día.
Hay que tener en cuenta que se trata sólo de una aproximación. El método sólo funciona si la base de los triángulos (A en el diagrama) es infinitamente pequeña.
EL EXPERIMENTO DE LA AGUJA DE BUFFON. Georges-Louis Leclerc, conde de Buffon (1707-1788)
La Aguja de Buffon se encuentra entre los más antiguos problemas en el campo de la probabilidad geométrica. Es uno de los más sorprendentes ejemplos que muestran cómo el número
π aparece en los lugares más insospechados. Buffon, en su enciclopedia de 44 volúmenes Histoire Naturelle, describió todo lo conocido sobre el mundo natural. En el apéndice, incluyó el problema (sin ninguna relación con la historia natural) del experimento de la aguja. En Les Epoques de la Nature se atrevió a sugerir que el planeta tenía mucho más de los 6000 años que proclamaba la Iglesia. Se convirtió en el historiador más importante de su tiempo, con una gran influencia en muchos campos de la ciencia. A la edad de 20 años, Buffon descubrió el teorema del binomio, y más tarde introdujo el cálculo diferencial e integral en la teoría de la probabilidad.
LANZAMIENTO DE DARDOS
Aproximación al área del círculo
Otra forma de hallar una aproximación del área del círculo sería utilizar el método de Monte Carlo, que consiste en tirar dardos en un área cuadrada. El método de Monte Carlo utiliza números aleatorios y probabilidades para resolver problemas. Si se esparcen uniformemente varias muestras aleatorias sobre la superficie de un cuadrado en el que se ha inscrito un círculo, la proporción de blancos en el círculo se aproxima a la relación del área del círculo con la del cuadrado. Para obtener una aproximación satisfactoria es necesario utilizar un gran número de muestras aleatorias.
En nuestro experimento, lanzamos 800 dardos y obtuvimos el área del círculo con una precisión del 96 por ciento.
Páginas 130 y 131.
LA PARADOJA DEL ORIFICIO EN UNA ESFERA
Marilyn von Savant, famosa por el problema de Monty Hall en la revista Parade, publicó este problema. Si hacemos un agujero en forma de cilindro perfecto de 6 pulgadas de largo a través del centro de una esfera sólida de 6 pulgadas de diámetro, ¿cuál es el volumen de la esfera restante? Para hacer un agujero de 6 pulgadas de largo en una esfera más grande, habría que tener un taladro muy grueso que pudiera cortar dos tapas de la esfera y una gran parte de su volumen, dejando únicamente un anillo cilíndrico curvado, como un servilletero. Estos dibujos te darán algunas pistas para obtener la respuesta. Ahora, imaginemos que una broca gigante abre un agujero de 6 pulgadas a través de la Tierra, ¿qué quedaría de ella?
CÓCTEL LARGO
Estima visualmente, pero sin hacer ningún cálculo, qué es mayor, ¿la circunferencia del vaso del cóctel o su altura?
Mañana, día 14 del mes 3 se celebra el día de pi (π). No es nuestra notación: no me gusta (nada) la notación anglosajona.
Me encanta la estimación del "Cóctel largo", sobre todo para hacerlo en directo.
