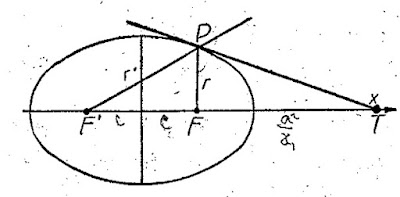Matemáticas 6º Curso

Matemáticas 6º Curso. Plan 1938


P. Puid Adam


Biblioteca matemática Rey Pastor-Puig Adam. 1950


Páginas 66 y 67
Resolución nomográfica de la ecuación de segundo grado
En lugar de representar la gráfica y=ax²+bx+c para cada ecuación ax²+bx+c=0, es mucho más práctico poner la ecuación en esta forma:

x²=-b/ax-c/a

o sea    x²=px+q

y la resolución gráfica se reduce a hallar los puntos comunes a la parábola y=x² y a la recta y=px+q, y leer su abscisa.
En efecto, hallar un valor de x que haga x²=px+q equivale a hallar la abscisa de un punto que tenga igual ordenada en la parábola y en la recta, es decir, del punto o puntos comunes.

Ejemplo: En la figura 39 se ha resuelto la ecuación 2x²‑8x‑54=0 o sea, x²=4x+27 y se obtienen gráficamente las raíces x₁=‑3,5, x₂=7,5.
Obsérvese la adopción de escalas distintas en ambos ejes, lo que ha dado una curva y=x² más abierta [...]; esto es conveniente para la claridad del dibujo.

La ventaja de este modo de proceder está en que se puede dibujar con cuidado la curva y=x², de una vez para todas, en papel milimetrado; y la resolución de cada caso particular se reduce así a determinar la recta y=px+q (lo que puede hacerse sin dibujarla, uniendo dos de sus puntos con una regla o hilo) y leer en el papel las coordenadas de los puntos comunes, si los tienen.


Páginas 115 y 116

La tangente en un punto a la elipse es la bisectriz del ángulo formado por un radio vector y la prolongación del otro.

En esta propiedad se funda la que tienen las bóvedas y los espejos reflectores elípticos de concentrar en un foco los rayos u ondas procedentes del otro foco.
Si la bóveda no es exactamente elíptica, no habrá un punto, sino una zona de concentración de ondas donde se oirá con mayor claridad.

Tal es el fenómeno que se observa en los cruces de bóvedas claustrales (rincón de los secretos de El Escorial), en las estaciones del Metro, en las que a veces una conversación en voz baja en un andén es oída con sorprendente claridad desde el foco correspondiente del otro andén. (Las bóvedas del Metro no son exactamente elípticas, pero tienen forma parecida.)

Dos curiosidades de la antigua enseñanza de las matemáticas.
La primera, la resolución nomográfica, es porque los cálculos se hacían, en el mejor de los casos, con reglas de cálculo como la que está junto a la portada del libro. Ahora, que en el teléfono móvil tenemos calculadora y hasta aplicaciones para dibujar funciones, este método resulta obsoleto pero es ingenioso.
La segunda es un ejemplo "práctico" de las elipses.
Pedro Puig Adam ya estuvo por aquí.
De la misma colección es este libro.